License
Attribution-ShareAlike 4.0 International
=======================================================================
Creative Commons Corporation ("Creative Commons") is not a law firm and
does not provide legal services or legal advice. Distribution of
Creative Commons public licenses does not create a lawyer-client or
other relationship. Creative Commons makes its licenses and related
information available on an "as-is" basis. Creative Commons gives no
warranties regarding its licenses, any material licensed under their
terms and conditions, or any related information. Creative Commons
disclaims all liability for damages resulting from their use to the
fullest extent possible.
Using Creative Commons Public Licenses
Creative Commons public licenses provide a standard set of terms and
conditions that creators and other rights holders may use to share
original works of authorship and other material subject to copyright
and certain other rights specified in the public license below. The
following considerations are for informational purposes only, are not
exhaustive, and do not form part of our licenses.
Considerations for licensors: Our public licenses are
intended for use by those authorized to give the public
permission to use material in ways otherwise restricted by
copyright and certain other rights. Our licenses are
irrevocable. Licensors should read and understand the terms
and conditions of the license they choose before applying it.
Licensors should also secure all rights necessary before
applying our licenses so that the public can reuse the
material as expected. Licensors should clearly mark any
material not subject to the license. This includes other CC-
licensed material, or material used under an exception or
limitation to copyright. More considerations for licensors:
wiki.creativecommons.org/Considerations_for_licensors
Considerations for the public: By using one of our public
licenses, a licensor grants the public permission to use the
licensed material under specified terms and conditions. If
the licensor's permission is not necessary for any reason--for
example, because of any applicable exception or limitation to
copyright--then that use is not regulated by the license. Our
licenses grant only permissions under copyright and certain
other rights that a licensor has authority to grant. Use of
the licensed material may still be restricted for other
reasons, including because others have copyright or other
rights in the material. A licensor may make special requests,
such as asking that all changes be marked or described.
Although not required by our licenses, you are encouraged to
respect those requests where reasonable. More considerations
for the public:
wiki.creativecommons.org/Considerations_for_licensees
=======================================================================
Creative Commons Attribution-ShareAlike 4.0 International Public
License
By exercising the Licensed Rights (defined below), You accept and agree
to be bound by the terms and conditions of this Creative Commons
Attribution-ShareAlike 4.0 International Public License ("Public
License"). To the extent this Public License may be interpreted as a
contract, You are granted the Licensed Rights in consideration of Your
acceptance of these terms and conditions, and the Licensor grants You
such rights in consideration of benefits the Licensor receives from
making the Licensed Material available under these terms and
conditions.
Section 1 -- Definitions.
a. Adapted Material means material subject to Copyright and Similar
Rights that is derived from or based upon the Licensed Material
and in which the Licensed Material is translated, altered,
arranged, transformed, or otherwise modified in a manner requiring
permission under the Copyright and Similar Rights held by the
Licensor. For purposes of this Public License, where the Licensed
Material is a musical work, performance, or sound recording,
Adapted Material is always produced where the Licensed Material is
synched in timed relation with a moving image.
b. Adapter's License means the license You apply to Your Copyright
and Similar Rights in Your contributions to Adapted Material in
accordance with the terms and conditions of this Public License.
c. BY-SA Compatible License means a license listed at
creativecommons.org/compatiblelicenses, approved by Creative
Commons as essentially the equivalent of this Public License.
d. Copyright and Similar Rights means copyright and/or similar rights
closely related to copyright including, without limitation,
performance, broadcast, sound recording, and Sui Generis Database
Rights, without regard to how the rights are labeled or
categorized. For purposes of this Public License, the rights
specified in Section 2(b)(1)-(2) are not Copyright and Similar
Rights.
e. Effective Technological Measures means those measures that, in the
absence of proper authority, may not be circumvented under laws
fulfilling obligations under Article 11 of the WIPO Copyright
Treaty adopted on December 20, 1996, and/or similar international
agreements.
f. Exceptions and Limitations means fair use, fair dealing, and/or
any other exception or limitation to Copyright and Similar Rights
that applies to Your use of the Licensed Material.
g. License Elements means the license attributes listed in the name
of a Creative Commons Public License. The License Elements of this
Public License are Attribution and ShareAlike.
h. Licensed Material means the artistic or literary work, database,
or other material to which the Licensor applied this Public
License.
i. Licensed Rights means the rights granted to You subject to the
terms and conditions of this Public License, which are limited to
all Copyright and Similar Rights that apply to Your use of the
Licensed Material and that the Licensor has authority to license.
j. Licensor means the individual(s) or entity(ies) granting rights
under this Public License.
k. Share means to provide material to the public by any means or
process that requires permission under the Licensed Rights, such
as reproduction, public display, public performance, distribution,
dissemination, communication, or importation, and to make material
available to the public including in ways that members of the
public may access the material from a place and at a time
individually chosen by them.
l. Sui Generis Database Rights means rights other than copyright
resulting from Directive 96/9/EC of the European Parliament and of
the Council of 11 March 1996 on the legal protection of databases,
as amended and/or succeeded, as well as other essentially
equivalent rights anywhere in the world.
m. You means the individual or entity exercising the Licensed Rights
under this Public License. Your has a corresponding meaning.
Section 2 -- Scope.
a. License grant.
1. Subject to the terms and conditions of this Public License,
the Licensor hereby grants You a worldwide, royalty-free,
non-sublicensable, non-exclusive, irrevocable license to
exercise the Licensed Rights in the Licensed Material to:
a. reproduce and Share the Licensed Material, in whole or
in part; and
b. produce, reproduce, and Share Adapted Material.
2. Exceptions and Limitations. For the avoidance of doubt, where
Exceptions and Limitations apply to Your use, this Public
License does not apply, and You do not need to comply with
its terms and conditions.
3. Term. The term of this Public License is specified in Section
6(a).
4. Media and formats; technical modifications allowed. The
Licensor authorizes You to exercise the Licensed Rights in
all media and formats whether now known or hereafter created,
and to make technical modifications necessary to do so. The
Licensor waives and/or agrees not to assert any right or
authority to forbid You from making technical modifications
necessary to exercise the Licensed Rights, including
technical modifications necessary to circumvent Effective
Technological Measures. For purposes of this Public License,
simply making modifications authorized by this Section 2(a)
(4) never produces Adapted Material.
5. Downstream recipients.
a. Offer from the Licensor -- Licensed Material. Every
recipient of the Licensed Material automatically
receives an offer from the Licensor to exercise the
Licensed Rights under the terms and conditions of this
Public License.
b. Additional offer from the Licensor -- Adapted Material.
Every recipient of Adapted Material from You
automatically receives an offer from the Licensor to
exercise the Licensed Rights in the Adapted Material
under the conditions of the Adapter's License You apply.
c. No downstream restrictions. You may not offer or impose
any additional or different terms or conditions on, or
apply any Effective Technological Measures to, the
Licensed Material if doing so restricts exercise of the
Licensed Rights by any recipient of the Licensed
Material.
6. No endorsement. Nothing in this Public License constitutes or
may be construed as permission to assert or imply that You
are, or that Your use of the Licensed Material is, connected
with, or sponsored, endorsed, or granted official status by,
the Licensor or others designated to receive attribution as
provided in Section 3(a)(1)(A)(i).
b. Other rights.
1. Moral rights, such as the right of integrity, are not
licensed under this Public License, nor are publicity,
privacy, and/or other similar personality rights; however, to
the extent possible, the Licensor waives and/or agrees not to
assert any such rights held by the Licensor to the limited
extent necessary to allow You to exercise the Licensed
Rights, but not otherwise.
2. Patent and trademark rights are not licensed under this
Public License.
3. To the extent possible, the Licensor waives any right to
collect royalties from You for the exercise of the Licensed
Rights, whether directly or through a collecting society
under any voluntary or waivable statutory or compulsory
licensing scheme. In all other cases the Licensor expressly
reserves any right to collect such royalties.
Section 3 -- License Conditions.
Your exercise of the Licensed Rights is expressly made subject to the
following conditions.
a. Attribution.
1. If You Share the Licensed Material (including in modified
form), You must:
a. retain the following if it is supplied by the Licensor
with the Licensed Material:
i. identification of the creator(s) of the Licensed
Material and any others designated to receive
attribution, in any reasonable manner requested by
the Licensor (including by pseudonym if
designated);
ii. a copyright notice;
iii. a notice that refers to this Public License;
iv. a notice that refers to the disclaimer of
warranties;
v. a URI or hyperlink to the Licensed Material to the
extent reasonably practicable;
b. indicate if You modified the Licensed Material and
retain an indication of any previous modifications; and
c. indicate the Licensed Material is licensed under this
Public License, and include the text of, or the URI or
hyperlink to, this Public License.
2. You may satisfy the conditions in Section 3(a)(1) in any
reasonable manner based on the medium, means, and context in
which You Share the Licensed Material. For example, it may be
reasonable to satisfy the conditions by providing a URI or
hyperlink to a resource that includes the required
information.
3. If requested by the Licensor, You must remove any of the
information required by Section 3(a)(1)(A) to the extent
reasonably practicable.
b. ShareAlike.
In addition to the conditions in Section 3(a), if You Share
Adapted Material You produce, the following conditions also apply.
1. The Adapter's License You apply must be a Creative Commons
license with the same License Elements, this version or
later, or a BY-SA Compatible License.
2. You must include the text of, or the URI or hyperlink to, the
Adapter's License You apply. You may satisfy this condition
in any reasonable manner based on the medium, means, and
context in which You Share Adapted Material.
3. You may not offer or impose any additional or different terms
or conditions on, or apply any Effective Technological
Measures to, Adapted Material that restrict exercise of the
rights granted under the Adapter's License You apply.
Section 4 -- Sui Generis Database Rights.
Where the Licensed Rights include Sui Generis Database Rights that
apply to Your use of the Licensed Material:
a. for the avoidance of doubt, Section 2(a)(1) grants You the right
to extract, reuse, reproduce, and Share all or a substantial
portion of the contents of the database;
b. if You include all or a substantial portion of the database
contents in a database in which You have Sui Generis Database
Rights, then the database in which You have Sui Generis Database
Rights (but not its individual contents) is Adapted Material,
including for purposes of Section 3(b); and
c. You must comply with the conditions in Section 3(a) if You Share
all or a substantial portion of the contents of the database.
For the avoidance of doubt, this Section 4 supplements and does not
replace Your obligations under this Public License where the Licensed
Rights include other Copyright and Similar Rights.
Section 5 -- Disclaimer of Warranties and Limitation of Liability.
a. UNLESS OTHERWISE SEPARATELY UNDERTAKEN BY THE LICENSOR, TO THE
EXTENT POSSIBLE, THE LICENSOR OFFERS THE LICENSED MATERIAL AS-IS
AND AS-AVAILABLE, AND MAKES NO REPRESENTATIONS OR WARRANTIES OF
ANY KIND CONCERNING THE LICENSED MATERIAL, WHETHER EXPRESS,
IMPLIED, STATUTORY, OR OTHER. THIS INCLUDES, WITHOUT LIMITATION,
WARRANTIES OF TITLE, MERCHANTABILITY, FITNESS FOR A PARTICULAR
PURPOSE, NON-INFRINGEMENT, ABSENCE OF LATENT OR OTHER DEFECTS,
ACCURACY, OR THE PRESENCE OR ABSENCE OF ERRORS, WHETHER OR NOT
KNOWN OR DISCOVERABLE. WHERE DISCLAIMERS OF WARRANTIES ARE NOT
ALLOWED IN FULL OR IN PART, THIS DISCLAIMER MAY NOT APPLY TO YOU.
b. TO THE EXTENT POSSIBLE, IN NO EVENT WILL THE LICENSOR BE LIABLE
TO YOU ON ANY LEGAL THEORY (INCLUDING, WITHOUT LIMITATION,
NEGLIGENCE) OR OTHERWISE FOR ANY DIRECT, SPECIAL, INDIRECT,
INCIDENTAL, CONSEQUENTIAL, PUNITIVE, EXEMPLARY, OR OTHER LOSSES,
COSTS, EXPENSES, OR DAMAGES ARISING OUT OF THIS PUBLIC LICENSE OR
USE OF THE LICENSED MATERIAL, EVEN IF THE LICENSOR HAS BEEN
ADVISED OF THE POSSIBILITY OF SUCH LOSSES, COSTS, EXPENSES, OR
DAMAGES. WHERE A LIMITATION OF LIABILITY IS NOT ALLOWED IN FULL OR
IN PART, THIS LIMITATION MAY NOT APPLY TO YOU.
c. The disclaimer of warranties and limitation of liability provided
above shall be interpreted in a manner that, to the extent
possible, most closely approximates an absolute disclaimer and
waiver of all liability.
Section 6 -- Term and Termination.
a. This Public License applies for the term of the Copyright and
Similar Rights licensed here. However, if You fail to comply with
this Public License, then Your rights under this Public License
terminate automatically.
b. Where Your right to use the Licensed Material has terminated under
Section 6(a), it reinstates:
1. automatically as of the date the violation is cured, provided
it is cured within 30 days of Your discovery of the
violation; or
2. upon express reinstatement by the Licensor.
For the avoidance of doubt, this Section 6(b) does not affect any
right the Licensor may have to seek remedies for Your violations
of this Public License.
c. For the avoidance of doubt, the Licensor may also offer the
Licensed Material under separate terms or conditions or stop
distributing the Licensed Material at any time; however, doing so
will not terminate this Public License.
d. Sections 1, 5, 6, 7, and 8 survive termination of this Public
License.
Section 7 -- Other Terms and Conditions.
a. The Licensor shall not be bound by any additional or different
terms or conditions communicated by You unless expressly agreed.
b. Any arrangements, understandings, or agreements regarding the
Licensed Material not stated herein are separate from and
independent of the terms and conditions of this Public License.
Section 8 -- Interpretation.
a. For the avoidance of doubt, this Public License does not, and
shall not be interpreted to, reduce, limit, restrict, or impose
conditions on any use of the Licensed Material that could lawfully
be made without permission under this Public License.
b. To the extent possible, if any provision of this Public License is
deemed unenforceable, it shall be automatically reformed to the
minimum extent necessary to make it enforceable. If the provision
cannot be reformed, it shall be severed from this Public License
without affecting the enforceability of the remaining terms and
conditions.
c. No term or condition of this Public License will be waived and no
failure to comply consented to unless expressly agreed to by the
Licensor.
d. Nothing in this Public License constitutes or may be interpreted
as a limitation upon, or waiver of, any privileges and immunities
that apply to the Licensor or You, including from the legal
processes of any jurisdiction or authority.
=======================================================================
Creative Commons is not a party to its public licenses.
Notwithstanding, Creative Commons may elect to apply one of its public
licenses to material it publishes and in those instances will be
considered the “Licensor.” The text of the Creative Commons public
licenses is dedicated to the public domain under the CC0 Public Domain
Dedication. Except for the limited purpose of indicating that material
is shared under a Creative Commons public license or as otherwise
permitted by the Creative Commons policies published at
creativecommons.org/policies, Creative Commons does not authorize the
use of the trademark "Creative Commons" or any other trademark or logo
of Creative Commons without its prior written consent including,
without limitation, in connection with any unauthorized modifications
to any of its public licenses or any other arrangements,
understandings, or agreements concerning use of licensed material. For
the avoidance of doubt, this paragraph does not form part of the public
licenses.
Creative Commons may be contacted at creativecommons.org.
Calculus of One Variable Functions
Key Terms
Function
A function is a rule that assigns a unique value
to each value
in a given domain.
The set of value taken by when takes all possible value in the domain is the range of .
Rational Functions
A function of the type
where and are polynomials, is called a rational function.
Its range has to exclude all those values of where .
Inverse Functions
Consider the function
.
If
is such that for each
in the range there is exactly one
in the domain, we can define the inverse
as:
Limits
Consider the following:
The value of the function can be easily calculated when
,
but when
,
we get the expression
.
However, when we evaluate
for values that approach 0, those values of
approach 1.
This suggests defining the limit of a function
to be the limiting value, if it exists, of
as
gets approaches
.
Limits from Above and Below
Sometimes approaching 0 with small positive values of gives you a different limit from approaching with small negative values of .
The limit you get from approaching 0 with positive values is known as the limit from above:
and with negative values is known as the limit from below:
If the two limits are equal, we simply refer to the limit.
Important Functions
Exponential Functions
It can also be written as an infinite series:
The two important limits to know are:
- as , ()
- as , ()
Note that for all real values of .
Hyperbolic Functions (sinh
and cosh)
The hyperbolic sine
()
and hyperbolic cosine function
()
are defined by:

Some key facts about these functions:
- has even symmetry and and have odd symmetry
- as , and
- ’s limits are -1 and +1
- Derivatives:
Natural Logarithm
Since the exponential of any real number is positive, the domain of is .
Implicit Functions
An implicit function takes the form
To draw the curve of an implicit function you have to rewrite it in the form . There may be more than one value for each value.
Differentiation
The derivative of the function is denoted by:
Geometrically, the derivative is the gradient of the curve .
It is a measure of the rate of change of as varies.
For example, velocity, , is the rate of change of displacement, , with respect to time, , or:
Formal Definition

As , the clospe of the cord slope of the tangent, or:
whenever this limit exists.
Rules for Differentiation
Powers
Trigonometric Functions
Exponential Functions
where and are constant.
Linearity
Product Rule
Quotient Rule
Chain Rule
Let
Example 1
Differentiate
.
Let ,
L’Hôpital’s Rule
l’Hôpital’s rule provides a systematic way of dealing with limits of functions like .
Suppose
and
and we want .
If
where any is any real number or , then
You can keep applying the rule until you get a sensible answer.
Graphs
Stationary Points
An important application of calculus is to find where a function is a maximum or minimum.
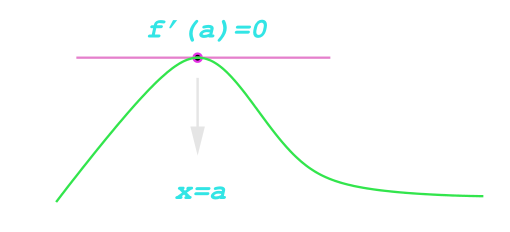
when these occur the gradient of the tangent to the curve, . The condition alone however does not guarantee a minimum or maximum. It only means that point is a stationary point.
There are three main types of stationary points:
- maximum
- minimum
- point of inflection
Local Maximum
The point is a local maximum if:
This is because is a decreasing function of near .
Local Minimum
The point is a local minimum if:
This is because is a increasing function of near .
Point of Inflection

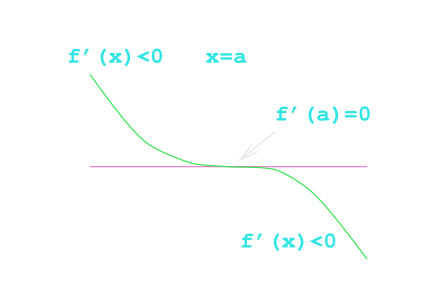
Approximating with the Taylor series
The expansion
is an example of a Taylor series. These enable us to approximate a given function f(x) using a series which is often easier to calculate. Among other uses, they help us:
- calculate complicated function using simple arithmetic operations
- find useful analytical approximations which work for near a given value (e.g. for near 0)
- Understand the behaviour of a function near a stationary point
Strategy
Suppose we know information about only at the point . How can we find out about for other values of ?
We could approximate the function by successive polynomials, each time matching more derivatives at .
Example 1
For
near 0, approximate
by a quadratic.
Set :
Set :
Set :
So for near 0,
Check:
| 0.4 | 0.921061 | 0.920 |
| 0.2 | 0.960066 | 0.980 |
| 0.1 | 0.995004 | 0.995 |
General Case
Maclaurin Series
A Maclaurin series is a Taylor series expansion of a function about 0.
Any function can be written as an infinite Maclaurin Series
where
( means evaluated at )
Taylor Series
We may alternatively expand about any point to give a Taylor series:
a generalisation of a Maclaurin series.
An alternative form of Taylor series is given by setting where is small:
Taylor Series at a Stationary Point
If f(x) has a stationary point at , then and the Taylor series begins
- If then the quadratic part makes the function increase going away from and we have a minimum
- If then the quadratic part makes the function decrease going away from and we have a maximum
- If then we must include a higer order terms to determine what happens have a minimum
Integration
Integration is the reverse of differentiation.
Take velocity and displacement as an example:
where is the constant of integration, which is required for indefinite integrals.A
Definite Integrals
The definite integral of a function in the range is denoted be:
If ( is the derivative of ) then
Area and Integration
Approximate the area under a smooth curve using a large number of narrow rectangles.

Area under curve .
As the rectangles get more numerous and narrow, the approximation approaches the real area.
The limiting value is denoted
This explains the notation used for integrals.
Example 1
Calculate the area between these two curves:

Find the crossing points and
Since between and
Techniques for Integration
Integration requires multiple techniques and methods to do correctly because it is a PITA.
These are best explained by examples so try to follow those rather than expect and explanation.
Integration by Substitution
Integration but substitution lets us integrate functions of functions.
Example 1
Find
Let
The integral is then
Finally substitute out
Example 2
Find
Let
Then
The integral is now
Finally substitute out to get:
Example 3
Find
Use the previous example to get to
Since the limits are:
This gives us
Example 4
Find
- Try a trigonmetrical substitution:
Therefore
But so:
Hence
Integration by Parts
or
This technique is derived from integrating the product rule.
Example 1
Find
Use
Set
and .This means that and .
Application of Integration
Differential Equations
Consider the equation
To find , is not a straightforward integration:
The equation above does not solve for as we can’t integrate the right until we know … which is what we’re trying to find.
This is an example of a first order differential equation. The general form is:
Separable Differential Equations
A first order diferential equation is called separable if it is of the form
We can solve these by rearranging:
Example 1
Find
such that
where
is a constant.
Rearrange to get
where is an arbitrary constant.
page rendered by gronk