title: MMME1048 // Fluid Dynamics

uuid: b88f78f8-a358-460b-9dbb-812e7b1ace92 (permalink)

tags: [ uni, nottingham, mechanical, engineering, fluid_mechanics, mmme1048, fluid_dynamics ]

written by: Alvie Rahman

syntax highlighting based on Pygments' default colors

page generated by gronk

License 
Attribution-ShareAlike 4.0 International

=======================================================================

Creative Commons Corporation ("Creative Commons") is not a law firm and
does not provide legal services or legal advice. Distribution of
Creative Commons public licenses does not create a lawyer-client or
other relationship. Creative Commons makes its licenses and related
information available on an "as-is" basis. Creative Commons gives no
warranties regarding its licenses, any material licensed under their
terms and conditions, or any related information. Creative Commons
disclaims all liability for damages resulting from their use to the
fullest extent possible.

Using Creative Commons Public Licenses

Creative Commons public licenses provide a standard set of terms and
conditions that creators and other rights holders may use to share
original works of authorship and other material subject to copyright
and certain other rights specified in the public license below. The
following considerations are for informational purposes only, are not
exhaustive, and do not form part of our licenses.

     Considerations for licensors: Our public licenses are
     intended for use by those authorized to give the public
     permission to use material in ways otherwise restricted by
     copyright and certain other rights. Our licenses are
     irrevocable. Licensors should read and understand the terms
     and conditions of the license they choose before applying it.
     Licensors should also secure all rights necessary before
     applying our licenses so that the public can reuse the
     material as expected. Licensors should clearly mark any
     material not subject to the license. This includes other CC-
     licensed material, or material used under an exception or
     limitation to copyright. More considerations for licensors:
     wiki.creativecommons.org/Considerations_for_licensors

     Considerations for the public: By using one of our public
     licenses, a licensor grants the public permission to use the
     licensed material under specified terms and conditions. If
     the licensor's permission is not necessary for any reason--for
     example, because of any applicable exception or limitation to
     copyright--then that use is not regulated by the license. Our
     licenses grant only permissions under copyright and certain
     other rights that a licensor has authority to grant. Use of
     the licensed material may still be restricted for other
     reasons, including because others have copyright or other
     rights in the material. A licensor may make special requests,
     such as asking that all changes be marked or described.
     Although not required by our licenses, you are encouraged to
     respect those requests where reasonable. More considerations
     for the public:
     wiki.creativecommons.org/Considerations_for_licensees

=======================================================================

Creative Commons Attribution-ShareAlike 4.0 International Public
License

By exercising the Licensed Rights (defined below), You accept and agree
to be bound by the terms and conditions of this Creative Commons
Attribution-ShareAlike 4.0 International Public License ("Public
License"). To the extent this Public License may be interpreted as a
contract, You are granted the Licensed Rights in consideration of Your
acceptance of these terms and conditions, and the Licensor grants You
such rights in consideration of benefits the Licensor receives from
making the Licensed Material available under these terms and
conditions.


Section 1 -- Definitions.

  a. Adapted Material means material subject to Copyright and Similar
     Rights that is derived from or based upon the Licensed Material
     and in which the Licensed Material is translated, altered,
     arranged, transformed, or otherwise modified in a manner requiring
     permission under the Copyright and Similar Rights held by the
     Licensor. For purposes of this Public License, where the Licensed
     Material is a musical work, performance, or sound recording,
     Adapted Material is always produced where the Licensed Material is
     synched in timed relation with a moving image.

  b. Adapter's License means the license You apply to Your Copyright
     and Similar Rights in Your contributions to Adapted Material in
     accordance with the terms and conditions of this Public License.

  c. BY-SA Compatible License means a license listed at
     creativecommons.org/compatiblelicenses, approved by Creative
     Commons as essentially the equivalent of this Public License.

  d. Copyright and Similar Rights means copyright and/or similar rights
     closely related to copyright including, without limitation,
     performance, broadcast, sound recording, and Sui Generis Database
     Rights, without regard to how the rights are labeled or
     categorized. For purposes of this Public License, the rights
     specified in Section 2(b)(1)-(2) are not Copyright and Similar
     Rights.

  e. Effective Technological Measures means those measures that, in the
     absence of proper authority, may not be circumvented under laws
     fulfilling obligations under Article 11 of the WIPO Copyright
     Treaty adopted on December 20, 1996, and/or similar international
     agreements.

  f. Exceptions and Limitations means fair use, fair dealing, and/or
     any other exception or limitation to Copyright and Similar Rights
     that applies to Your use of the Licensed Material.

  g. License Elements means the license attributes listed in the name
     of a Creative Commons Public License. The License Elements of this
     Public License are Attribution and ShareAlike.

  h. Licensed Material means the artistic or literary work, database,
     or other material to which the Licensor applied this Public
     License.

  i. Licensed Rights means the rights granted to You subject to the
     terms and conditions of this Public License, which are limited to
     all Copyright and Similar Rights that apply to Your use of the
     Licensed Material and that the Licensor has authority to license.

  j. Licensor means the individual(s) or entity(ies) granting rights
     under this Public License.

  k. Share means to provide material to the public by any means or
     process that requires permission under the Licensed Rights, such
     as reproduction, public display, public performance, distribution,
     dissemination, communication, or importation, and to make material
     available to the public including in ways that members of the
     public may access the material from a place and at a time
     individually chosen by them.

  l. Sui Generis Database Rights means rights other than copyright
     resulting from Directive 96/9/EC of the European Parliament and of
     the Council of 11 March 1996 on the legal protection of databases,
     as amended and/or succeeded, as well as other essentially
     equivalent rights anywhere in the world.

  m. You means the individual or entity exercising the Licensed Rights
     under this Public License. Your has a corresponding meaning.


Section 2 -- Scope.

  a. License grant.

       1. Subject to the terms and conditions of this Public License,
          the Licensor hereby grants You a worldwide, royalty-free,
          non-sublicensable, non-exclusive, irrevocable license to
          exercise the Licensed Rights in the Licensed Material to:

            a. reproduce and Share the Licensed Material, in whole or
               in part; and

            b. produce, reproduce, and Share Adapted Material.

       2. Exceptions and Limitations. For the avoidance of doubt, where
          Exceptions and Limitations apply to Your use, this Public
          License does not apply, and You do not need to comply with
          its terms and conditions.

       3. Term. The term of this Public License is specified in Section
          6(a).

       4. Media and formats; technical modifications allowed. The
          Licensor authorizes You to exercise the Licensed Rights in
          all media and formats whether now known or hereafter created,
          and to make technical modifications necessary to do so. The
          Licensor waives and/or agrees not to assert any right or
          authority to forbid You from making technical modifications
          necessary to exercise the Licensed Rights, including
          technical modifications necessary to circumvent Effective
          Technological Measures. For purposes of this Public License,
          simply making modifications authorized by this Section 2(a)
          (4) never produces Adapted Material.

       5. Downstream recipients.

            a. Offer from the Licensor -- Licensed Material. Every
               recipient of the Licensed Material automatically
               receives an offer from the Licensor to exercise the
               Licensed Rights under the terms and conditions of this
               Public License.

            b. Additional offer from the Licensor -- Adapted Material.
               Every recipient of Adapted Material from You
               automatically receives an offer from the Licensor to
               exercise the Licensed Rights in the Adapted Material
               under the conditions of the Adapter's License You apply.

            c. No downstream restrictions. You may not offer or impose
               any additional or different terms or conditions on, or
               apply any Effective Technological Measures to, the
               Licensed Material if doing so restricts exercise of the
               Licensed Rights by any recipient of the Licensed
               Material.

       6. No endorsement. Nothing in this Public License constitutes or
          may be construed as permission to assert or imply that You
          are, or that Your use of the Licensed Material is, connected
          with, or sponsored, endorsed, or granted official status by,
          the Licensor or others designated to receive attribution as
          provided in Section 3(a)(1)(A)(i).

  b. Other rights.

       1. Moral rights, such as the right of integrity, are not
          licensed under this Public License, nor are publicity,
          privacy, and/or other similar personality rights; however, to
          the extent possible, the Licensor waives and/or agrees not to
          assert any such rights held by the Licensor to the limited
          extent necessary to allow You to exercise the Licensed
          Rights, but not otherwise.

       2. Patent and trademark rights are not licensed under this
          Public License.

       3. To the extent possible, the Licensor waives any right to
          collect royalties from You for the exercise of the Licensed
          Rights, whether directly or through a collecting society
          under any voluntary or waivable statutory or compulsory
          licensing scheme. In all other cases the Licensor expressly
          reserves any right to collect such royalties.


Section 3 -- License Conditions.

Your exercise of the Licensed Rights is expressly made subject to the
following conditions.

  a. Attribution.

       1. If You Share the Licensed Material (including in modified
          form), You must:

            a. retain the following if it is supplied by the Licensor
               with the Licensed Material:

                 i. identification of the creator(s) of the Licensed
                    Material and any others designated to receive
                    attribution, in any reasonable manner requested by
                    the Licensor (including by pseudonym if
                    designated);

                ii. a copyright notice;

               iii. a notice that refers to this Public License;

                iv. a notice that refers to the disclaimer of
                    warranties;

                 v. a URI or hyperlink to the Licensed Material to the
                    extent reasonably practicable;

            b. indicate if You modified the Licensed Material and
               retain an indication of any previous modifications; and

            c. indicate the Licensed Material is licensed under this
               Public License, and include the text of, or the URI or
               hyperlink to, this Public License.

       2. You may satisfy the conditions in Section 3(a)(1) in any
          reasonable manner based on the medium, means, and context in
          which You Share the Licensed Material. For example, it may be
          reasonable to satisfy the conditions by providing a URI or
          hyperlink to a resource that includes the required
          information.

       3. If requested by the Licensor, You must remove any of the
          information required by Section 3(a)(1)(A) to the extent
          reasonably practicable.

  b. ShareAlike.

     In addition to the conditions in Section 3(a), if You Share
     Adapted Material You produce, the following conditions also apply.

       1. The Adapter's License You apply must be a Creative Commons
          license with the same License Elements, this version or
          later, or a BY-SA Compatible License.

       2. You must include the text of, or the URI or hyperlink to, the
          Adapter's License You apply. You may satisfy this condition
          in any reasonable manner based on the medium, means, and
          context in which You Share Adapted Material.

       3. You may not offer or impose any additional or different terms
          or conditions on, or apply any Effective Technological
          Measures to, Adapted Material that restrict exercise of the
          rights granted under the Adapter's License You apply.


Section 4 -- Sui Generis Database Rights.

Where the Licensed Rights include Sui Generis Database Rights that
apply to Your use of the Licensed Material:

  a. for the avoidance of doubt, Section 2(a)(1) grants You the right
     to extract, reuse, reproduce, and Share all or a substantial
     portion of the contents of the database;

  b. if You include all or a substantial portion of the database
     contents in a database in which You have Sui Generis Database
     Rights, then the database in which You have Sui Generis Database
     Rights (but not its individual contents) is Adapted Material,

     including for purposes of Section 3(b); and
  c. You must comply with the conditions in Section 3(a) if You Share
     all or a substantial portion of the contents of the database.

For the avoidance of doubt, this Section 4 supplements and does not
replace Your obligations under this Public License where the Licensed
Rights include other Copyright and Similar Rights.


Section 5 -- Disclaimer of Warranties and Limitation of Liability.

  a. UNLESS OTHERWISE SEPARATELY UNDERTAKEN BY THE LICENSOR, TO THE
     EXTENT POSSIBLE, THE LICENSOR OFFERS THE LICENSED MATERIAL AS-IS
     AND AS-AVAILABLE, AND MAKES NO REPRESENTATIONS OR WARRANTIES OF
     ANY KIND CONCERNING THE LICENSED MATERIAL, WHETHER EXPRESS,
     IMPLIED, STATUTORY, OR OTHER. THIS INCLUDES, WITHOUT LIMITATION,
     WARRANTIES OF TITLE, MERCHANTABILITY, FITNESS FOR A PARTICULAR
     PURPOSE, NON-INFRINGEMENT, ABSENCE OF LATENT OR OTHER DEFECTS,
     ACCURACY, OR THE PRESENCE OR ABSENCE OF ERRORS, WHETHER OR NOT
     KNOWN OR DISCOVERABLE. WHERE DISCLAIMERS OF WARRANTIES ARE NOT
     ALLOWED IN FULL OR IN PART, THIS DISCLAIMER MAY NOT APPLY TO YOU.

  b. TO THE EXTENT POSSIBLE, IN NO EVENT WILL THE LICENSOR BE LIABLE
     TO YOU ON ANY LEGAL THEORY (INCLUDING, WITHOUT LIMITATION,
     NEGLIGENCE) OR OTHERWISE FOR ANY DIRECT, SPECIAL, INDIRECT,
     INCIDENTAL, CONSEQUENTIAL, PUNITIVE, EXEMPLARY, OR OTHER LOSSES,
     COSTS, EXPENSES, OR DAMAGES ARISING OUT OF THIS PUBLIC LICENSE OR
     USE OF THE LICENSED MATERIAL, EVEN IF THE LICENSOR HAS BEEN
     ADVISED OF THE POSSIBILITY OF SUCH LOSSES, COSTS, EXPENSES, OR
     DAMAGES. WHERE A LIMITATION OF LIABILITY IS NOT ALLOWED IN FULL OR
     IN PART, THIS LIMITATION MAY NOT APPLY TO YOU.

  c. The disclaimer of warranties and limitation of liability provided
     above shall be interpreted in a manner that, to the extent
     possible, most closely approximates an absolute disclaimer and
     waiver of all liability.


Section 6 -- Term and Termination.

  a. This Public License applies for the term of the Copyright and
     Similar Rights licensed here. However, if You fail to comply with
     this Public License, then Your rights under this Public License
     terminate automatically.

  b. Where Your right to use the Licensed Material has terminated under
     Section 6(a), it reinstates:

       1. automatically as of the date the violation is cured, provided
          it is cured within 30 days of Your discovery of the
          violation; or

       2. upon express reinstatement by the Licensor.

     For the avoidance of doubt, this Section 6(b) does not affect any
     right the Licensor may have to seek remedies for Your violations
     of this Public License.

  c. For the avoidance of doubt, the Licensor may also offer the
     Licensed Material under separate terms or conditions or stop
     distributing the Licensed Material at any time; however, doing so
     will not terminate this Public License.

  d. Sections 1, 5, 6, 7, and 8 survive termination of this Public
     License.


Section 7 -- Other Terms and Conditions.

  a. The Licensor shall not be bound by any additional or different
     terms or conditions communicated by You unless expressly agreed.

  b. Any arrangements, understandings, or agreements regarding the
     Licensed Material not stated herein are separate from and
     independent of the terms and conditions of this Public License.


Section 8 -- Interpretation.

  a. For the avoidance of doubt, this Public License does not, and
     shall not be interpreted to, reduce, limit, restrict, or impose
     conditions on any use of the Licensed Material that could lawfully
     be made without permission under this Public License.

  b. To the extent possible, if any provision of this Public License is
     deemed unenforceable, it shall be automatically reformed to the
     minimum extent necessary to make it enforceable. If the provision
     cannot be reformed, it shall be severed from this Public License
     without affecting the enforceability of the remaining terms and
     conditions.

  c. No term or condition of this Public License will be waived and no
     failure to comply consented to unless expressly agreed to by the
     Licensor.

  d. Nothing in this Public License constitutes or may be interpreted
     as a limitation upon, or waiver of, any privileges and immunities
     that apply to the Licensor or You, including from the legal
     processes of any jurisdiction or authority.


=======================================================================

Creative Commons is not a party to its public licenses.
Notwithstanding, Creative Commons may elect to apply one of its public
licenses to material it publishes and in those instances will be
considered the “Licensor.” The text of the Creative Commons public
licenses is dedicated to the public domain under the CC0 Public Domain
Dedication. Except for the limited purpose of indicating that material
is shared under a Creative Commons public license or as otherwise
permitted by the Creative Commons policies published at
creativecommons.org/policies, Creative Commons does not authorize the
use of the trademark "Creative Commons" or any other trademark or logo
of Creative Commons without its prior written consent including,
without limitation, in connection with any unauthorized modifications
to any of its public licenses or any other arrangements,
understandings, or agreements concerning use of licensed material. For
the avoidance of doubt, this paragraph does not form part of the public
licenses.

Creative Commons may be contacted at creativecommons.org.

Introductory Concepts

These are ideas you need to know about to know what’s going on, I guess?

Control Volumes

A control volume is a volume with an imaginary boundary to make it easier to analyse the flow of a fluid. The boundary is drawn where the properties and conditions of the fluid is known, or where an approximation can be made. Properties which may be know include:

The region in the control volume is analysed in terms of energy and mass flows entering and leaving the control volumes. You don’t have to understand what’s going on inside the control volume.

Example 1

The thrust of a jet engine on an aircraft at rest can be analysed in terms of the changes in momentum or the air passing through the engine.

The control volume is drawn far enough in front of the engine that the air velocity entering can be assumed to be at atmospheric pressure and its velocity negligible.

At the exit of the engine the boundary is drawn close where the velocity is known and the air pressure atmospheric.

The control volume cuts the material attaching the engine to the aircraft and there will be a force transmitted across the control volume there to oppose the forces on the engine created by thrust and gravity.

The details of the flows inside the control volume do not need to be known as the thrust can be determined in terms of forces and flows crossing the boundaries drawn. However, to understand the flows inside the engine in more detail, a more detailed analysis would be required.

Ideal Fluid

The actual flow pattern in a fluid is usually complex and difficult to model but it can be simplified by assuming the fluid is ideal. The ideal fluid has the following properties:

Gases and vapours are compressible so can only be analysed as ideal fluids when flow velocities are low but they can often be treated as ideal (or perfect) gases, in which case the ideal gas equations apply.

Steady Flow

Steady flow is a flow which has no changes in properties with respect to time. Properties may vary from place to place but in the same place the properties must not change in the control volume to be steady flow.

Unsteady flow does change with respect to time.

Uniform Flow

Uniform flow is when all properties are the same at all points at any given instant but can change with respect to time, like the opposite of steady flow.

One Dimensional Flow

In one dimensional (1D) flow it is assumed that all properties are uniform over any plane perpendicular to the direction of flow (e.g. all points along the cross section of a pipe have identical properties).

This means properties can only flow in one direction—usually the direction of flow.

1D flow is never achieved exactly in practice as when a fluid flows along a pipe, the velocity at the wall is 0, and maximum in the centre of the pipe. Despite this, assuming flow is 1D simplifies the analysis and often is accurate enough.

Flow Patterns

There are multiple ways to visualize flow patterns.

Streamlines

A streamline is a line along which all the particle have, at a given instant, velocity vectors which are tangential to the line.

Therefore there is no component of velocity of a streamline.

A particle can never cross a streamline and streamlines never cross.

They can be constructed mathematically and are often shown as output from CFD analysis.

For a steady flow there are no changes with respect to time so the streamline pattern does not. The pattern does change when in unsteady flow.

Streamlines in uniform flow must be straight and parallel. They must be parallel as if they are not, then different points will have different directions and therefore different velocities. Same reasoning with if they are not parallel.

Pathlines

A pathline shows the route taken by a single particle during a given time interval. It is equivalent to a high exposure photograph which traces the movement of the particle marked. You could track pathlines with a drop of injected dye or inserting a buoyant solid particle which has the same density as the solid.

Pathlines may cross.

Streaklines

A streakline joins, at any given time, all particles that have passed through a given point. Examples of this are line dye or a smoke stream which is produced from a continuous supply.

Viscous (Real) Fluids

Viscosity

A fluid offers resistance to motion due to its viscosity or internal friction. The greater the resistance to flow, the greater the viscosity.

Higher viscosity also reduces the rate of shear deformation between layers for a given shear stress.

Viscosity comes from two effects:

Newton’s Law of Viscosity

Viscosity can be defined in terms of rate of shear or velocity gradient.

Consider the flow in the pipe above. Fluid in contact with the surface has a velocity of 0 because the surface irregularities trap the fluid particles. A short distance away from the surface the velocity is low but in the middle of the pipe the velocity is vFv_F.

Let the velocity at a distance yy be vv and at a distance y+δyy + \delta y be v+δvv + \delta v.

The ratio δvδy\frac{\delta v}{\delta y} is the average velocity gradient over the distance δy\delta y.

But as δy\delta y tends to zero, δvδy→\frac{\delta v}{\delta y} \rightarrow the value of the differential dvdy\frac{\mathrm{d}v}{\mathrm{d}y} at a point such as point A.

For most fluids in engineering it is found that the shear stress, τ\tau, is directly proportional to the velocity gradient when straight and parallel flow is involved:

τ=μdvdy\tau = \mu\frac{\mathrm{d}v}{\mathrm{d}y}

Where μ\mu is the constant of proportionality and known as the dynamic viscosity, or simply the viscosity of the fluid.

This is Newton’s Law of Viscosity and fluids that obey it are known as Newtonian fluids.

Viscosity and Lubrication

Where a fluid is a thin film (such as in lubricating flows), the velocity gradient can be approximated to be linear and an estimate of shear stress obtained:

τ=μδvδy≈μvy\tau = \mu \frac{\delta v}{\delta y} \approx \mu \frac{v}{y}

From the shear stress we can calculate the force exerted by a film by the relationship:

τ=FA\tau = \frac F A

Fluid Flow

Types of flow

There are essentially two types of flow:

Between fully laminar and fully turbulent flows is a transition region.

The Reynolds Number

Development of the Reynolds Number

In laminar flow the most influential factor is the magnitude of the viscous forces:

viscousforces∝μvll2=μvlviscous\, forces \propto \mu\frac v l l^2 = \mu vl

where vv is a characteristic velocity and ll is a characteristic length.

In turbulent flow viscous effects are not significant but inertia effects (mixing, momentum exchange, acceleration of fluid mass) are. Inertial forces can be represented by F=maF = ma

m∝ρl3a=dvdt∴a∝vt and t=lv∴a∝v2l∴Interial forces∝ρl2v2l=ρl2v2\begin{align*} m &\propto \rho l^3 \\ a &= \frac{dv}{dt} \\ &\therefore a \propto \frac v t \text{ and } t = \frac l v \\ &\therefore a \propto \frac {v^2} l \\ &\therefore \text{Interial forces} \propto \rho l^2\frac{v^2} l = \rho l^2v^2 \end{align*}

The ratio of internal forces to viscous forces is called the Reynolds number and is abbreviated to Re:

Re=interial forcesviscous forces=ρl2v2μvl=ρvlμ\text{Re}= \frac{\text{interial forces}}{\text{viscous forces}} = \frac {\rho l^2v^2}{\mu vl} = \frac {\rho vl} \mu

where ρ\rho and μ\mu are fluid properties and vv and ll are characteristic velocity and length.

is a non dimensional group. It has no units because the units cancel out.

Non dimensional groups are very important in fluid mechanics and need to be considered when scaling experiments.

If is the same in two different pipes, the flow will be the same regardless of actual diameters, densities, or other properties.

for a Circular Section Pipe

The characteristic length for pipe flow is the diameter dd and the characteristic velocity is mean flow in the pipe, vv, so of a circular pipe section is given by:

Re=ρvdμ\text{Re}= \frac{\rho vd} \mu

For flow in a smooth circular pipe under normal engineering conditions the following can be assumed:

These figures can be significantly affected by surface roughness so flow may be turbulent below Re=4000\text{Re}= 4000.

Euler’s Equation

In a static fluid, pressure only depends on density and elevation. In a moving fluid the pressure is also related to acceleration, viscosity, and shaft work done on or by the fluid.

1ρδpδs+gδzδs+vδvδs=0\frac 1 \rho \frac{\delta p}{\delta s} + g\frac{\delta z}{\delta s} + v\frac{\delta v}{\delta s} = 0

Assumptions / Conditions

The Euler equation applies where the following can be assumed:

Bernoulli’s Equation

Euler’s equation comes in differential form, which is difficult to apply. We can integrate it to make it easier

1ρδpδs+gδzδs+vδvδs=0(Euler’s equation)∫{dpρ+gdz+vdv}=∫0ds∴∫1ρdp+g∫dz+∫vdv=∫0ds∴∫1ρdp+gz+v22=constant1\begin{align*} \frac 1 \rho \frac{\delta p}{\delta s} + g\frac{\delta z}{\delta s} + v\frac{\delta v}{\delta s} &= 0 & \text{(Euler's equation)} \\ \int\left\{\frac{\mathrm{d}p} \rho + g\mathrm{d}z + v\mathrm{d}v \right\} &= \int 0 \,\mathrm{d}s \\ \therefore \int \frac 1 \rho \,\mathrm{d}p + g\int \mathrm{d}z + \int v \,\mathrm{d}v &= \int 0 \,\mathrm{d}s \\ \therefore \int \frac 1 \rho \,\mathrm{d}p + gz + \frac{v^2}{2} &= \text{constant}_1 \end{align*}

The first term of the equation can only be integrated if ρ\rho is constant as then:

∫1ρdp=1ρ∫dp=pρ\int \frac 1 \rho \,\mathrm{d}p = \frac 1 \rho \int \mathrm{d}p = \frac p \rho

So, if density is constant:

pρ+gz+v22=constant2\frac p \rho + gz + \frac{v^2}{2} = \text{constant}_2

Assumptions / Conditions

All the assumptions from Euler’s equation apply:

But also one more:

Forms of Bernoulli’s Equation

Energy Form

This form of Bernoulli’s Equation is known as the energy form as each component has the units energy/unit mass:

pρ+gz+v22=constant2\frac p \rho + gz + \frac{v^2}{2} = \text{constant}_2

It is split into 3 parts:

Elevation / Head Form

Divide the energy form by gg:

pρg+z+v22g=HT\frac p {\rho g} + z + \frac{v^2}{2g} = H_T

where HTH_T is constant and:

Pressure Form

Multiply the energy form by ρ\rho to give the pressure form:

p+ρgz+12ρv2=constantp + \rho gz + \frac 1 2 \rho v^2 = \text{constant}

where:

Comparing two forms of the Bernoulli Equation (Piezometric)

piezometric=static+elevation\text{piezometric} = \text{static} + \text{elevation}

Pressure form:

ps+ρgz+12ρv2=total pressureps+ρgz=piezometric pressure\begin{align*} p_s + \rho gz + \frac 1 2 \rho v^2 &= \text{total pressure} \\ p_s + \rho gz &= \text{piezometric pressure} \end{align*}

Head form:

psρg+z+v22g=total headpsρg+z=piezometric head\begin{align*} \frac{p_s}{\rho g} + z + \frac{v^2}{2g} &= \text{total head} \\ \frac{p_s}{\rho g} + z &= \text{piezometric head} \end{align*}

Steady Flow Energy Equation (SFEE) and the Extended Bernoulli Equation (EBE)

SFEE is a more general equation that can be applied to any fluid and also is also takes heat energy into account. This is useful in applications such as a fan heater, jet engines, ICEs, and steam turbines.

The equation deals with 3 types of energy transfer:

  1. Thermal energy transfer (e.g. heat transfer from central heating to a room)
  2. Work energy transfer (e.g. shaft from car engine that turns wheels)
  3. Energy transfer in fluid flows (e.g. heat energy in a flow, potential energy in a flow, kinetic energy in a flow)

Derivation of Steady Flow Energy Equation

Consider a control volume with steady flows in and out and steady transfers of work and heat.

The properties don’t change with time at any any location and are considered uniform over inlet and outlet areas A1A_1 and A2A_2.

For steady flow, the mass, mm, of the fluid within the control volume and the total energy, EE, must be constant.

EE includes all forms for energy but we only consider internal, kinetic, and potential energy.

Consider a small time interval δt\delta t.

During δt\delta t, mass δm1\delta m_1 enters the control volume and δm2\delta m_2 leaves:

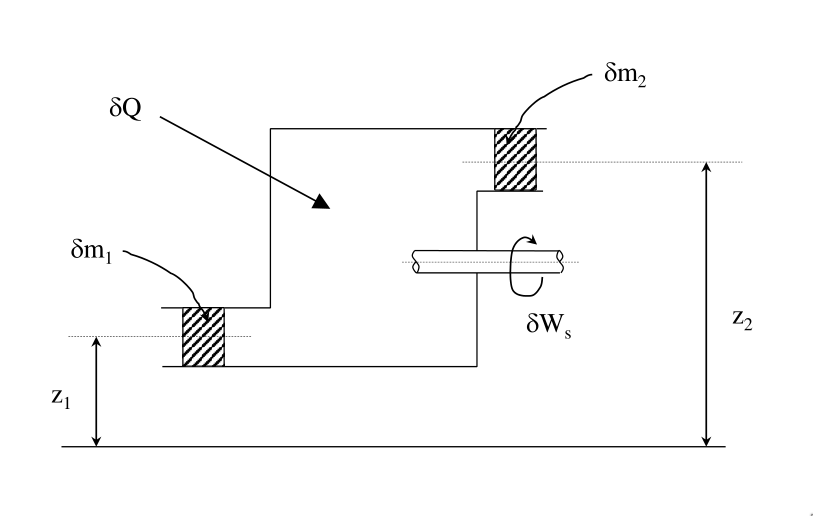
The specific energy e1e_1 of fluid δm1\delta m_1 is the sum of the specific internal energy, specific kinetic energy, and specific potential energy:

e1=u1+v122gz1e_1 = u_1 + \frac{v_1^2}{2} gz_1 e2=u2+v222gz2e_2 = u_2 + \frac{v_2^2}{2} gz_2

Since the mass is constant in the control volume, δm1=δm2\delta m_1 = \delta m_2.

Applying the First Law of Thermodynamics

The control volume is a system for which δE1\delta E_1 is added and δE2\delta E_2 is removed::

δE=δE2−δE1\delta E = \delta E_2 - \delta E_1

EE is constant so applying the first law of thermodynamics we know that:

δQ+δW=δE\delta Q + \delta W = \delta E

We can also say that:

δE=δE2−δE1=δm(e2−e1)\delta E = \delta E_2 - \delta E_1 = \delta m(e_2 - e_1)

The Work Term

The work term, δW\delta W, is made up of shaft work and the work necessary to deform the system (by adding δm1\delta m_1 at the inlet and removing δm2\delta m_2 at the outlet):

δW=δWs+net flow work\delta W = \delta W_s + \text{net flow work}

Work is done on the system by the mass entering and by the system on the mass leaving.

For example, at the inlet:

work done on system=force×distance=p1A1δx=p1δV1\text{work done on system} = \text{force} \times \text{distance} = p_1A_1\delta x = p_1\delta V_1

Knowing this, we can write:

δW=δWs+(p1δV1−p2δV2)\delta W = \delta W_s + (p_1\delta V_1 - p_2\delta V_2)

Back to the First Law

Substituting these equations:

δE=δE2−δE1=δm(e2−e1)\delta E = \delta E_2 - \delta E_1 = \delta m(e_2 - e_1) δW=δWs+(p1δV1−p2δV2)\delta W = \delta W_s + (p_1\delta V_1 - p_2\delta V_2)

into:

δQ+δW=δE\delta Q + \delta W = \delta E

gives us:

δQ+[δWs+(p1δV1−p2δV2)]=δm(e2−e1)\delta Q + \left[ \delta W_s + (p_1\delta V_1 - p_2\delta V_2)\right] = \delta m (e_2-e_1)

Dividing everything by δm\delta m and with a bit of rearranging we get:

q+ws=e2−e1+p2ρ2−p1ρ1q + w_s = e_2-e_1 + \frac{p_2}{\rho_2} - \frac{p_1}{\rho_1}

Substitute Back for ee

e=u+v22+gze = u + \frac{v^2}{2} + gz

This gives us:

q+ws+[u2+p2ρ2+gz2+v222]−[u1+p1ρ1+gz1+v122]q + w_s + \left[ u_2 + \frac{p_2}{\rho_2} + gz_2 + \frac{v_2^2}{2} \right] - \left[ u_1 + \frac{p_1}{\rho_1} + gz_1 + \frac{v_1^2}{2} \right]

Rearrange and Substitute for Enthalpy

By definition, enthalpy h=u+pv=u+pρh = u + pv = u + \frac p \rho. This gives us the equation:

q+ws=(h2−h1)+g(z2−z1)+v22−v122q + w_s = (h_2 - h_1) + g(z_2-z_1) + \frac{v_2^2-v_1^2}{2}

This equation is in specific energy form.

Multiplying by mass flow rate will give you the power form.

Application of the Steady Flow Energy Equation

Heat Transfer Devices

Like heat exchangers, boilers, condensers, and furnaces.

In this case, Ẇ=0\dot W = 0, δz0\delta z ~ 0, and δv20\delta v^2 ~ 0 so the equation can be simplified to just

Q̇=ṁ(h2−h1)=ṁcp(T2−T1)\dot Q = \dot m(h_2-h_1) = \dot m c_p(T_2-T_1)

Throttle Valve

No heat and work transfer. Often you can neglect potential and kinetic energy terms, giving you:

0=h2−h1)0 = h_2-h_1)

Work Transfer Devices

e.g. Turbines, Pumps, Fans, and Compressors

For these there is often no heat transfer (Q̇=0\dot Q = 0) and we can neglect potential (δz0\delta z ~ 0) and kinetic (δv20\delta v^2 ~ 0) energy terms, giving us the equation

Ẇ=ṁ(h2−h1)=ṁcp(T2−T1)\dot W = \dot m (h_2-h_1) = \dot m c_p(T_2-T_1)

Mixing Devices

e.g. Hot and cold water in a shower

In these processes, work and heat transfers are not important and you can often neglect potential and kinetic energy terms, giving us the same equation as for the throttle valve earlier:

0=h2−h10 = h_2-h_1

which you may want to write more usefully as:

∑ṁhout=∑ṁhin\sum \dot m h_{out} = \sum \dot m h_{in}

SFEE for Incompressible Fluids and Extended Bernoulli Equation

wsg=HT2−HT1+[(u2−u1)−1g]\frac{w_s}{g} = H_{T2} - H_{T1} + \left[ \frac{(u_2-u_1)-1}{g}\ \right]

or

ws=g(HT2−HT1+Hfw_s = g(H_{T2}-H_{T1}+H_f

If we assume shaft work, wsw_s, is 0, then we can get this equation:

HT1−HT2=HfH_{T1}-H_{T2} = H_f

This is very similar to the Bernoulli equation. The difference is that it considers friction so it can be applied to real fluids, not just ideal ones. It is called the Extended Bernoulli Equation.

The assumptions remain:

HfH_f for Straight Pipes

Hf=4fLDv22gH_f = \frac{4fL}{D} \frac{v^2}{2g}

Δp=ρgHf (pressure form)\Delta p = \rho g H_f \text{ (pressure form)}

This equation applies to long, round and straight pipes. It applies to both laminar and turbulent flow.

However be aware that in North America the equation is:

Hf=fLDv22gH_f = f \frac{L}{D} \frac{v^2}{2g}

Their ff (the Darcy Friction Factor) is four times our ff (Fanning Friction Factor). In mainland Europe, they use λ=4fFanning\lambda = 4f_{Fanning}, which is probably the least confusing version to use.

Finding ff

ff for Laminar Flow

f=16Ref = \frac{16}{\text{Re}}

ff for Turbulent Flow

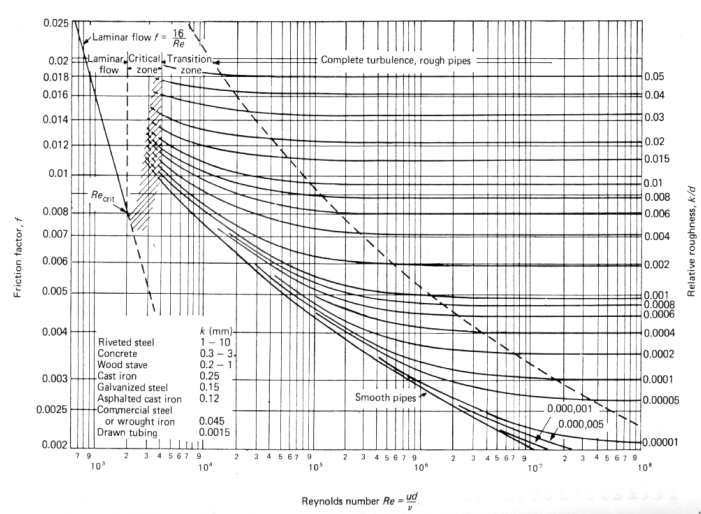
For turbulent flow, the value defends on relative pipe roughness (k′=kdk' = \frac k d) and Reynolds number.

Note when calculating k′k' that both kk and dd are measured in mm for some reason.

A Moody Chart is used to find ff:

A Moody Chart

Hydraulic Diameter

Dh=4×duct areaperimeterD_h = \frac{4 \times \text{duct area}}{\text{perimeter}}

Loss Factor KK

There are many parts of the pipe where losses can occur.

It is convenient to represent these losses in terms of loss factor, KK, times the velocity head:

Hf=Kv2gH_f = K \frac{v^2}{g}

Most manufacturers include loss factors in their data sheets.

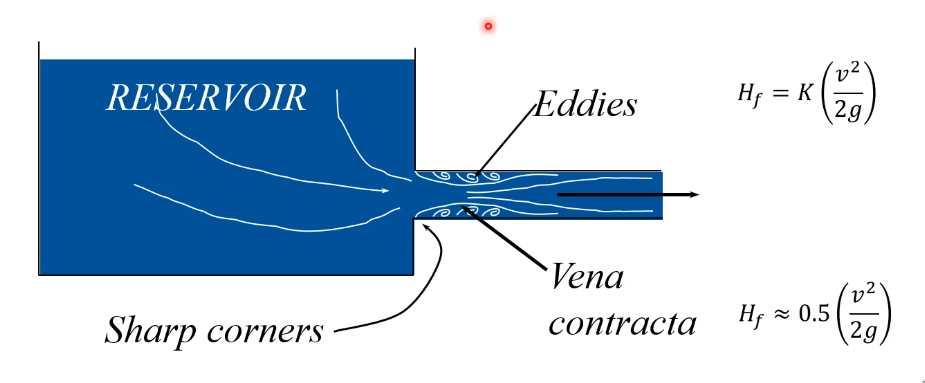
Loss Factor of Entry

Loss Factor of Expansion

K=(A2A1−1)2K = \left( \frac{A_2}{A_1} - 1\right)^2

This also tells us the loss factor on exit is basically 1.

For conical expansions, K0.08K ~ 0.08 (15 degrees cone angle), K0.25K ~ 0.25 (30 degrees). For cones you use the inlet velocity.

Loss Factor of Contraction

d2d1\frac{d_2}{d_1} K
0 0.5
0.2 0.45
0.4 0.38
0.6 0.28
0.8 0.14
1.0 0

Loss Factor of Pipe Bends

On a sharp bend, K0.9K ~ 0.9.

On a bend with a radius, K0.16−0.35K ~ 0.16-0.35.

Loss Factor of Nozzle

K0.05K ~ 0.05

But you use the outlet velocity, increasing losses.

page generated by gronk